1. Quanto valem hoje US$1.000.000,00 a serem entregues dentro de 20 anos a uma taxa de juros de 20%?
R: O que a questão pede, é exatamente a definição do valor-presente, definido da seguinte forma pelo Varian:
"O valor presente é a única forma correta de converter determinado fluxo de pagamentos em unidades monetárias de hoje".
Em termos matemáticos, o valor presente pode então ser definido como
Onde x é o valor futuro para o qual se analisa o valor presente, r é a taxa de juros (considerada constante) à qual tal valor é analisado, e t é o número de períodos no qual corre tal valor.
Sendo assim, para a questão dada teríamos:
que corresponde à US$26.084,0533.
No livro, o Varian, ou seja lá quem tenha editado os exercícios, foi preguiçoso, e deu uma resposta baseada na tabela 10.1 do capítulo 10, onde ele calcula o valor presente de US$1,00 para vários períodos.
No caso, para US$1,00 a ser pago daqui a vinte anos o valor presente corresponderia a US$0,03. O autor então pegou esse valor e o multiplicou por 1.000.000,00 obtendo o valor de US$30.000.000,00 (quase US$4.000,00 de diferença!). Esse erro ocorre porque na tabela os valores foram arredondados para duas casas decimais, o valor mais preciso seria 0,0260840533045888, que possui diferença insignificante no contexto de US$1,00. Porém, no contexto de US$1.000.000,00 a diferença se torna consideravelmente grande. Este é um bom exemplo de que não podemos desprezar pequenas imprecisões em determinados contextos.
2. À medida que a taxa de juros aumenta, a restrição orçamentária intertemporal torna-se mais íngreme ou mais plana?
R: Observe a curva de restrição orçamentária intertemporal:
Se atente aos interceptos. O que ocorre no eixo C2 se r aumenta? No caso, r entre multiplicando m1 (a dotação do primeiro período), aumentando assim o valor, logo o intercepto se deslocará para cima. No caso do eixo C1, r entra dividindo m2 (a dotação do segundo período), e se r aumentar então, reduzirá esse valor, deslocando para a direita esse intercepto. Sendo assim, a curva deverá se tornar mais íngreme.
3. A hipótese de que os bens sejam substitutos perfeitos deveria valer num estudo sobre as compras intertemporais de alimentos?
R: A hipótese de bens substitutos perfeitos em escolhas intertemporais se refere ao caso em que traçamos curvas de indiferença com uma inclinação constante de -1, logo, elas representarão os gostos de um consumidor que não se importa entre consumir hoje ou amanhã. Sua taxa marginal de substituição entre hoje e amanhã seria de -1. Pela própria definição fica claro que o consumidor não possui essa opção em relação à alimentos, já que esses devem ser consumidos todos os dias (ninguem é indiferente almoçar hoje e amanhã ou "não almoçar hoje e almoçar duas vezes amanhã".)
4. Um consumidor, que começou como emprestador, continua a ser emprestador mesmo após o declínio da taxa de juros. Como estará a situação desse consumidor após a variação da taxa de juros: melhor ou pior? E se o consumidor tornar-se tomador de empréstimos após a variação, ficará melhor ou pior situação?
R: Um indivíduo que seja emprestador possui a seguinte caracterização do seu ponto ótimo de consumo (tangente da sua curva de indiferença e sua restrição orçamentária intertemporal):
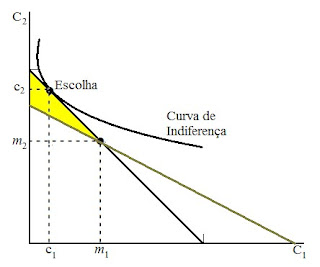
Nesse gráfico, estamos dizendo que o indivíduo consome menos do que a sua dotação orçamentária, e logo, dá como destino à sua sobre orçamentária o empréstimo. A questão está dizendo que o sujeito continua emprestando após a queda da taxa de juros (o que em tese, é um desestimulo ao empréstimo). Como vimos no exemplo anterior, se a taxa de juros aumenta, a curva de restrição orçamentária intertemporal se torna mais íngreme, e logo, para o inverso (diminuição da taxa de juros), essa curva se torna mais plana. Quando há uma mudança na taxa de juros, a curva de restrição orçamentária gira tendo como pivô o ponto de dotação inicial do indivíduo (afinal sua renda nominal não mudara). Logo, o seguinte gráfico ilustra essa situação:
Observe que, se o sujeito continua como emprestador, a curva de indiferença que tocará a sua curva de restrição deverá obrigatoriamente passar pela área amarela. Logo, ela não terá como estar acima da curva de indiferença anterior (esse exemplo não perde em generalidade). Logo, o sujeito estará numa condição pior (uma vez que estará numa curva de indiferença inferior).
5. Qual o valor presente de US$100,00 daqui a um ano, à taxa de juros de 10%? E qual o valor presente se a taxa for de 5%?
R: Como na primeira questão, podemos utilizar a seguinte fórmula:
À 10% teremos:
À 5% teremos:







Faltou a resposta da segunda pergunta da questão 4... =(
ResponderExcluirCapítulo 10, questão 5, à taxa de 10% a resposta aproximada é 90,91 e não 90,10 como está escrito ai.
ResponderExcluir